서론
미적분은 인공지능 등의 정보과학 분야에서는 자주 사용하지만, 알고리즘과 그 응용에 대한 분야에서는 잘 사용되지 않는다. 현장에서 사용되는 미적분 알고리즘에 대해 조사해보던 중 몬테카를로 적분을 알게 되었고, 이에 대해 탐구해 보고자 한다. 몬테카를로 적분(이하 MC 적분)에 대해 학습하고 python으로 분석한 뒤, 더 나은 알고리즘으로 발전시켜보고자 한다.
배경
1) Introduction of Monte Carlo integration
몬테카를로 적분(이하 MC적분)은 난수를 이용하여 적분값을 근사하는 기술이다. 주로 다차원의 정적분 문제를 효율적으로 해결하기 위해 사용된다. 정적분값 I를 근사하는 과정은 아래와 같다.

수식을 그림으로 이해해 보자. 정적분의 결과 I(회색 면적)을 구하기 위해 직사각형 모양의 주황색 면적의 평균을 구하는 것이다.

질문 1 : Monte Carlo integration이 구분구적법보다 효율적인가?
(1) 문제 제시
MC적분의 기본 원리는 구분구적법과 유사하다. 2차원 xy평면에서 n의 크기에 따른 오차율 감소 정도는 구분구적법이 더 크다. 그럼에도 불구하고 MC적분을 사용하는 이유가 무엇일까? MC적분을 주로 다차원 공간에서 사용한다고 알려져 있으므로, 차원이 증가할수록 구분구적법보다 MC적분이 효율적일 것이라는 가설을 세웠다. 다차원에서 구분구적법과 MC적분의 시간복잡도를 계산 해 보고 파이썬으로 구현해 보고자 한다.
(2) 수학적 과정
① 목표
임의의 3차원, 4차원 그래프를 설정하고 정적분 결과를 구해 참값으로 사용한다.
② 3차원 그래프
3차원 그래프 f(x,y)=x^2+y^2 가 있다. x,y의 범위가 각각 [-3, 3]로 주어졌을 때 그래프 아래 면적을 구해 보자.
구분구적법으로 표현하면 그래프 아래 면적은 다음과 같다.

정적분으로 표현하면 그래프 아래 면적은 다음과 같다.

설정한 3차원 그래프의 정적분 결과는 216이다.
③ 4차원 그래프
4차원 그래프 f(x,y,z)=sin(x+y+z)가 있다. x,y,z의 범위가 각각 [0,𝛑]로 주어졌을 때 그래프 아래 면적을 구해 보자.
구분구적법으로 표현하면 그래프 아래 면적은 다음과 같다.

정적분으로 표현하면 그래프 아래 면적은 다음과 같다.

설정한 3차원 그래프의 정적분 결과는 -8이다.
(3) Python 구현
① 목표
(2) 에서 얻은 참값을 바탕으로 구분구적법과 MC적분의 오차율 감소를 비교하자. python으로 각각을 구현하고 n값의 증가에 따른 오차 감소 정도를 그래프로 표현한다.
② 구분구적법의 python 구현
순서대로 3차원, 4차원의 예시이다.
def function(x, y):
return x ** 2 + y ** 2
def rienmann_sum(n):
t = 6 / n
volume = 0
for i in range(1, n + 1):
for j in range(1, n + 1):
volume += function(-3 + t * i, -3 + t * j) * t ** 2
return volume
import math
def function(x, y, z):
return math.sin(x + y + z)
def rienmann_sum(n):
t = math.pi / n
volume = 0
for i in range(1, n + 1):
for j in range(1, n + 1):
for k in range(1, n + 1):
volume += function(t * i, t * j, t * k) * t ** 3
return volume
③ MC 적분의 python 구현
순서대로 3차원, 4차원의 예시이다.
import random
def function(x, y):
return x ** 2 + y ** 2
def monte_carlo_integral(min_, max_, n):
total = 0
for _ in range(n):
x = random.uniform(min_, max_)
y = random.uniform(min_, max_)
total += function(x, y)
area = (max_ - min_) ** 2
return area * total / n
import random
import math
def function(x, y, z):
return math.sin(x+y+z)
def monte_carlo_integral(min_, max_, n):
total = 0
for _ in range(n):
x = random.uniform(min_, max_)
y = random.uniform(min_, max_)
z = random.uniform(min_, max_)
total += function(x, y, z)
area = (max_ - min_) ** 3
return area * total / n
(4) 결과
오차율 공식은 다음과 같다.

소요시간에 따른 오차율 그래프는 다음과 같다. python의 matplotlib 라이브러리를 활용하여 그래프를 시각화했다.


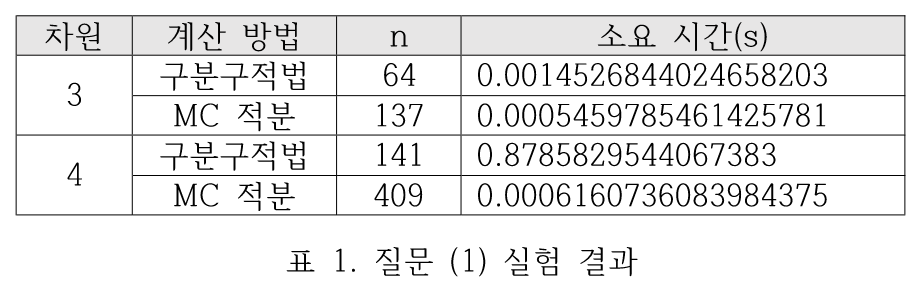
목표 오차율이 0.05%일 때 계산 방법에 따른 소요 시간을 구했다. MC적분은 무작위성을 갖기 때문에 반복실험 후 평균을 구했다.
(5) 결과 분석
구분구적법은 n의 차원-1 제곱만큼 반복시행한다. 따라서 차원이 증가할수록 소요시간이 크게 증가하였다. 반면 MC 적분의 반복시행횟수는 차원에 영향을 받지 않는다. pycharm 환경에서 실험한 결과 (표 1) 3차원에서는 구분구적법과 MC적분이 유의미한 소요 시간 차이를 보이지 않았으나 4차원에서는 1000배 이상의 차이를 보였다.
질문 2 : Monte Carlo integration의 오차 수렴 속도를 더 줄일 수는 없을까?
(1) 문제 제시
MC 적분을 시행하면서 발견된 문제점이 있다. MC 적분은 난수의 무작위성을 기반으로 오차가 발생하는데, 난수의 밀도가 불규칙한 경우 오차율이 증가한다. 이로 인해 같은 오차율임에도 불구하고 반복횟수가 크게 차이나는 경우가 많이 존재한다. (추가적으로 평균을 이용해 데이터를 다시 처리해야하는 번거로움이 존재한다.) 이 문제를 해결하기 위해 오차 수렴 속도를 줄일 방법을 고안할 필요를 느꼈고, 자료조사 중 quasi-Monte Carlo integration (이하 q-MC 적분)에 대해 알게 되었다. q-MC 적분을 간단하게 구현 및 시각화 하고 MC 적분과 오차 수렴 속도를 비교해보고자 한다.
(2) 수학적 과정
위의 문제를 해결하기 위해 준난수열을 도입한다. 준난수열이란 집합에 있는 기존 숫자로부터 가능한 한 멀리 떨어져 있는 연속된 수열이다.
선형 합동 생성기란 유사 난수 생성기의 일종으로, 순열 를 반환한다. 선형 합동 생성는 다음과 같다.

선형 합동 생성기가 생성해 내는 난수의 질은 설정한 인자에 따라 차이가 크게 발생한다. a=1, m=1인 특수한 경우 위 수열은 준난수열이 된다. C가 황금비의 소수부일 때 성능이 좋다는 사실이 자명하게 알려져 있으므로, 이를 이용해 준난수열을 생성한다. 수열의 정렬에 무작위성을 부여하여 준난수로 이루어진 좌표를 생산한다.
(3) Python 구현
① 목표
(2) 에서 설계한 구상한 코드( 각각 0이상 이하인 난수 좌표 1000개)를 python으로 구현한다. 구현한 난수 좌표를 기존에 사용하던 난수 좌표와 분포 정도를 비교한다. 오차 수렴 속도의 변화를 그래프로 시각화한다.
② 기존 난수 생성 코드
import random
import math
li1 = [random.uniform(0, math.pi) for _ in range(1000)]
li2 = [random.uniform(0, math.pi) for _ in range(1000)]
③ 준난수 생성 코드
def linear_congruential_generator(seed, a, c, m):
while True:
seed = (a * seed + c) % m
yield seed
def random_uniform_pi(a=1, c=0.61803398, m=1):
pi_range = math.pi
gen = linear_congruential_generator(0, a, c, m)
while True:
random_value = next(gen) / m
yield random_value * pi_range
(4) 결과
난수 생성 결과를 2차원 평면에 표현한 결과는 다음과 같다.
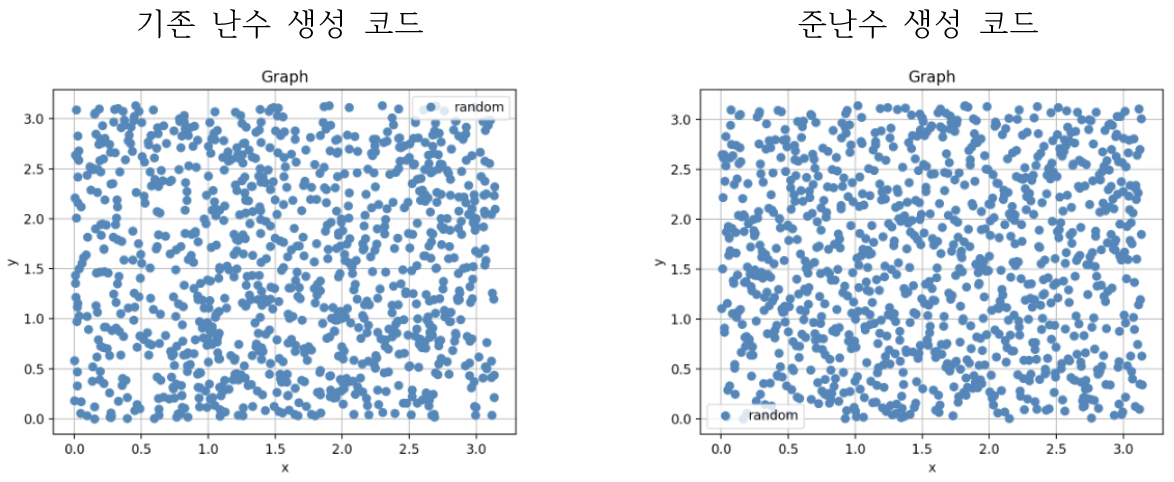
소요시간에 따른 오차율 그래프는 다음과 같다. python의 matplotlib 라이브러리를 활용하여 그래프를 시각화했다.

(5) 결과 분석
q-MC 적분은 기존 MC 적분보다 효율적으로 오차율을 줄일 수 있었다. 더 적은 반복시행으로 오차율을 빠르게 감소시켰으며, 각 오차율 사이의 편차가 적어 추가적인 평균 계산이 필요하지 않았다. 그러나 초기 준난수를 설정하는 값에 따라 수렴하는 오차율의 값이 상이하다는 단점이 존재하였다.
결론
차원이 증가할수록 구분구적법은 반복시행횟수가 지수적으로 증가하는 반면 MC적분을 사용할 경우 반복횟수가 크게 증가하지 않는다. 이를 이용해 다차원의 정적분 근사에서 MC적분이 자주 사용된다. 준난수를 이용한 q-MC적분을 다면 오차 수렴속도를 줄일 수 있지만, 초기 준난수의 설정에 따라 그 효율에서 차이가 발생한다. 준난수의 suffle을 고르게 시행하는 것으로 위의 문제를 해결할 수 있을 것이다. MC적분은 확률 및 경제에서 응용될 수 있으며, 컴퓨터그래픽이나 3D렌더링 분야에서 지속적으로 사용될 것이다.
'[Journal]' 카테고리의 다른 글
| [Journal] 미분 응용 - Python으로 경사하강법 구현하기 (2) | 2023.12.02 |
|---|---|
| [Journal] 제2코사인법칙 응용 - 뉴스 분류 알고리즘 (0) | 2023.10.27 |
| [Journal] 반복로그 (log*) (0) | 2023.09.18 |
| [Journal] 점근표기법과 시간복잡도 (0) | 2023.09.10 |
| [Journal] 단백질 구조 예측 알고리즘 AlphaFold2 - 소개와 원리 (0) | 2023.08.30 |



