서론
정보과학 분야에서 미분을 응용한 사례가 있는지 알아보고자 하였다. 경사하강법에서 미분을 사용해 최적해를 구한다는 것을 알았고, 이를 파이썬으로 구현 해보고자 한다.
이론적 배경
편미분
편미분이란 다변수 함수의 특정 변수를 제외한 나머지 변수를 상수로 간주하여 미분하는 것이다. 예를 들어보자. 를 에 대해 편미분한 결과는 다음과 같이 표현될 수 있다.

기울기
함수 f가 모든 변수에 대해 편미분 가능할 경우, f의 기울기는 각 변수에 대한 편미분을 좌표로 갖는 벡터이다.
경사하강법
경사 하강법은 1차 근삿값 발견용 최적화 알고리즘이다. 함수의 기울기(경사)를 구하고 경사의 반대 방향으로 계속 이동시켜 극값에 이를 때까지 반복시키는 것이다. 복잡하고 비선형적이어서 미분을 통해 극값을 구하기 어려운 경우 유용하게 최적해를 찾을 수 있다.

최적화할 함수 f에 대하여 시작점 x_0를 정한다. 점 x_i에 대하여 그 다음으로 이동할 점 x_i+1은 다음과 같이 구한다.
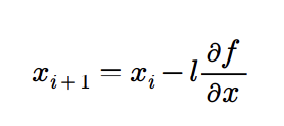
l은 상수값으로, 학습률(learning_rate)를 의미한다. 학습률은 기울기를 상수 배 할 때 사용한다. 학습률이 너무 작다면 주어진 반복횟수 내에 최적해에 도달하지 못하고, 학습률이 너무 크다면 탐색범위 밖으로 발산할 수 있다. 따라서 예비 실행을 통해 적절한 학습률을 설정해야한다.
미분 구현
미분은 평균변화율의 극한(순간변화율)이다. 수식으로 표현하면 다음과 같다.

이 순간변화율을 구하는 수식을 파이썬으로 구현할 때 크게 두 가지의 문제가 발생한다. 첫째, 극한을 표현할 방법이 없기 때문에 h에 매우 작은 값을 입력하는 것으로 순간변화율을 어림해야 한다. 이때 컴퓨터는 소수점 연산에서 반올림을 사용하기 때문에 h에 매우 작은 값을 입력하면 최종 계산 결과에서 오차가 발생한다. 적절한 h값()을 선정해야한다. 둘째, h를 무한히 0에 가깝게 좁히는 것이 불가능하기 때문에 전방차분 대신 중앙차분을 사용해야한다. 이를 적용해 파이썬으로 미분을 구현했다. 추가적으로 접선을 그리는 함수를 구현했다.
직접 구현한 함수에 대한 자세한 설명(Table 1)은 아래와 같다.
Table 1 (1_미분계산.py 함수 설명)
| function(x) | 임의의 일변수함수를 설정했다. 사용자로부터 입력을 받는 인터페이스를 구현하는 것은 생략했다. |
| derivative(f, x) | 함수와 순간변화율을 구할 x값을 입력받으면 순간변화율을 반환한다. 중앙차분을 이용해 구현했다. |
| get_tangent(f, x) | 함수와 접선을 구할 x값을 입력받으면 접선의 방정식 반환한다. derivative(f, x)를 사용해 접선의 기울기를 구하고, 입력받은 함수를 이용해 y절편을 구한다. |
| main | 출력 범위를 설정하고 함수와 접선, 순간변화율을 출력한다. |
아래는 1_미분계산.py 코드 전문이다.
import numpy as np # 수치 계산에 사용되는 라이브러리
import matplotlib.pylab as plt # 그래프 출력에 사용되는 라이브러리
# 임의의 함수를 설정
def function(x):
return 2 * (x*x) + 3 * x + 4
# 중앙차분을 이용한 미분 구현
def derivative(f, x):
h = 1e-4
return (f(x+h) - f(x-h)) / (2*h)
# 접선을 구함
def get_tangent(f, x):
d = derivative(f, x) # 수치미분값 (접선의 기울기 의미)
y = f(x) - d * x # 접선의 절편
return lambda t: d * t + y # 접선의 함수 t 반환
# 출력 범위 설정 및 그래프 출력
if __name__ == '__main__':
a = int(input("순간변화율을 구할 x값 입력 : "))
print(derivative(function, a))
plt.xlabel('x')
plt.ylabel('f(x)')
x = np.arange(0.0, 20.0, 0.1)
y1 = function(x)
y2 = get_tangent(function, a)(x) # 접선의 함수 반환
plt.plot(x, y1) # 함수 f(x)
plt.plot(x, y2) # 접선
plt.show()

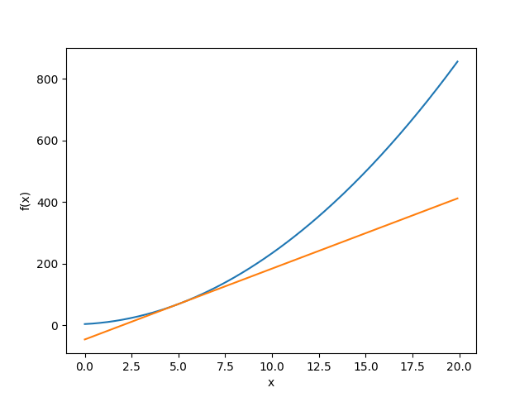
실행 결과 정상적으로 순간변화율과 접선이 출력되었고, 검산 결과(23)와 일치했다.
경사하강법 구현
직접 구현한 함수에 대한 자세한 설명(Table 2)은 아래와 같다.
Table 2 (2_편미분계산.py 함수 설명)
| function(x, y) | x, y를 변수로 갖는 임의의 이변수함수를 설정했다. 사용자로부터 입력을 받는 인터페이스를 구현하는 것은 생략했다. 각각의 변수들을 배열로 묶어서 설정하도록 코드를 수정한다면, 미지수 개수가 주어진 임의의 다변수함수에 대해서도 실행이 가능하다. |
| partial_derivative (f, x, y) |
함수와 x, y를 입력받으면 모든 변수에 대해 편미분을 실행하고, 결과값들을 하나의 배열로 묶어서 반환한다. 이변수함수이기에 반복문을 사용하지 않았지만, 미지수가 많아진다면 반복문으로 코드를 수정하여 사용한다. |
| gradient_descent(f, l, lr, step_num) | 함수, 변수 배열(l), 학습률(lr), 반복횟수(step_num)를 입력받는다. 수치하강을 반복횟수만큼 실행하며 변수 배열을 갱신한다. 갱신되는 과정과 최종적으로 수렴하는 좌표를 반환한다. |
| main | 수치하강을 실행할 초기 위치, 학습률, 반복횟수를 설정한다. gradient_descent(f, l, lr, step_num)를 실행한다. 함수가 최솟값을 가질 때 까지 변수가 갱신되는 과정을 그래프로 출력한다.(아래 코드에서는 이변수함수이기 때문에 2차원 그래프가 그려졌다.) 수치하강 결과 도달한 x, y값과 이때의 최솟값을 출력한다. |
아래는 2_편미분계산.py 코드 전문이다.
import numpy as np
import matplotlib.pylab as plt
# 임의의 다변수 함수를 설정
def function(x, y):
return (x ** 2) + (x * y) - 5 * x - 4 * y + (y ** 2)
# f(x,y) = x^2 + xy - 5x - 4y + y^2
# 편미분 구현
def partial_derivative(f, x, y):
# 넘파이 배열 x의 각 원소에 대해 미분한다.
h = 1e-4
grad = [0, 0]
grad[0] = (f(x+h, y) - f(x-h, y)) / (2 * h)
grad[1] = (f(x, y+h) - f(x, y-h)) / (2 * h)
return grad
# 경사하강법
def gradient_descent(f, l, lr, step_num):
l_history = []
for i in range(step_num):
l_history.append(l.copy()) # 시각화 하기 위함
grad = partial_derivative(f, l[0], l[1])
l[0] -= lr * grad[0]
l[1] -= lr * grad[1]
return l, np.array(l_history)
# 출력 범위 설정 및 그래프 출력
if __name__ == '__main__':
state = np.array([9.0, 8.0]) # x_0 설정 (초기상태)
lr = 0.1 # 적당한 상수값을 임의로 배정함
step_num = 100
state, l_history = gradient_descent(function, state, lr, step_num)
print("x = {}\ny = {}".format(state[0], state[1])) # 함수가 최솟값을 가질 때의 x, y값
print("Min : {}".format(function(state[0], state[1]))) # 최솟값
plt.plot([-10, 10], [0, 0], '--b')
plt.plot([0, 0], [-10, 10], '--b')
plt.plot(l_history[:, 0], l_history[:, 1], 'o')
plt.xlim(-10.5, 10.5) # x축 출력 범위
plt.ylim(-10.5, 10.5) # y축 출력 범위
plt.xlabel("X")
plt.ylabel("Y")
plt.show()
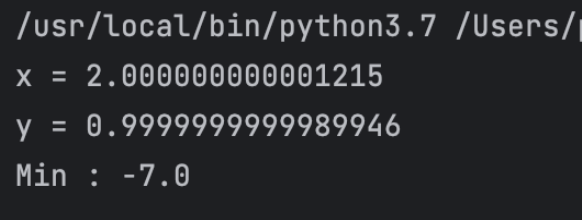

검산
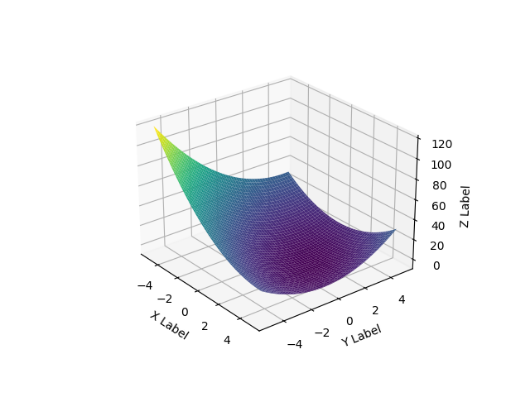
다변수함수를 시각화하는 프로그램을 간단하게 작성하고, 위에서 설정한 함수를 입력했다. 삼차원 그래프가 그려졌고, 수치하강을 통해 구한 (2,1)에서 최솟값을 갖는 것을 확인할 수 있었다.
아래는 다변수함수시각화.py 코드 전문이다.
import numpy as np
import matplotlib.pyplot as plt
def f(x, y):
return (x ** 2) + (x * y) - 5 * x - 4 * y + (y ** 2)
# 데이터 생성
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
x, y = np.meshgrid(x, y)
z = f(x, y)
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x, y, z, cmap='viridis')
# 축 레이블 설정
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
plt.show()
결론
순간변화율과 접선의 그래프, 수치하강의 과정과 최적해를 구하는 프로그램을 성공적으로 구현했고 오류 없이 동작했다. 미분의 정의를 그대로 코드에 적용시킨 것이기 때문에 로그함수, 지수함수 등 다항함수가 아닌 경우에서도 적용 가능하다는 장점이 있다. 사용자 인터페이스를 구축한다면 일반인을 대상으로 접근성이 좋아질 것이다. 변수의 개수를 입력받고 변수마다 반복하여 편미분하도록 코드를 수정한다면 모든 경우에 대해서 다룰 수 있을 것이다. 추가적으로, 유효숫자를 고려해 문제를 해결하도록 설정하는 것으로 협정참값을 더 효과적으로, 더 빠른 시간 안에 구할 수 있다.
'[Journal]' 카테고리의 다른 글
| [Journal] 적분 응용 - python을 이용한 몬테카를로 적분의 구현 (1) | 2024.04.07 |
|---|---|
| [Journal] 제2코사인법칙 응용 - 뉴스 분류 알고리즘 (0) | 2023.10.27 |
| [Journal] 반복로그 (log*) (0) | 2023.09.18 |
| [Journal] 점근표기법과 시간복잡도 (0) | 2023.09.10 |
| [Journal] 단백질 구조 예측 알고리즘 AlphaFold2 - 소개와 원리 (0) | 2023.08.30 |



